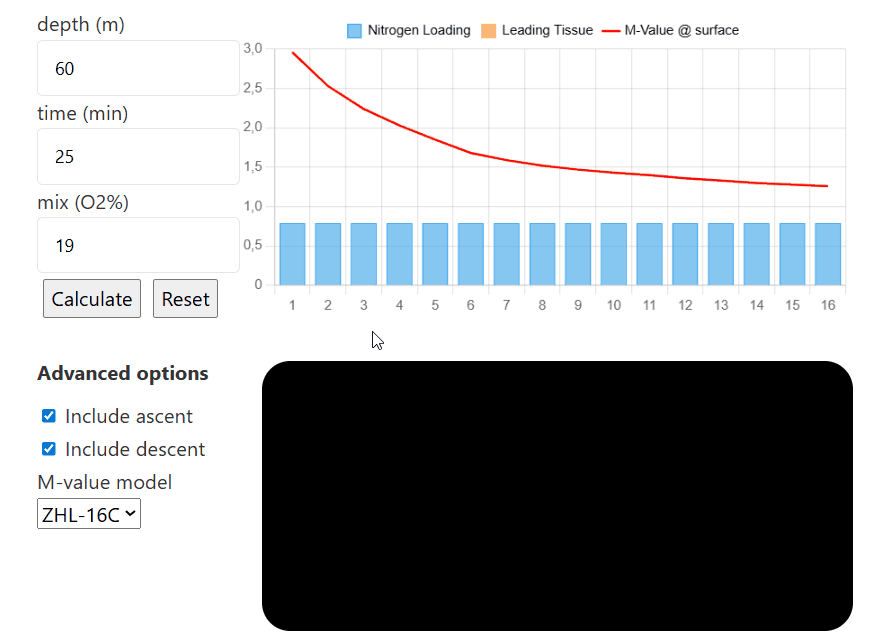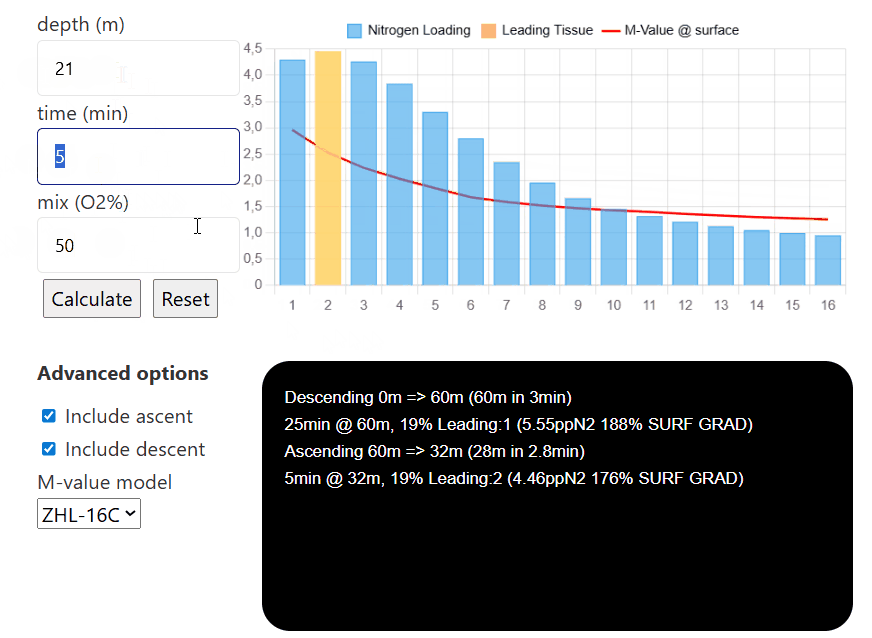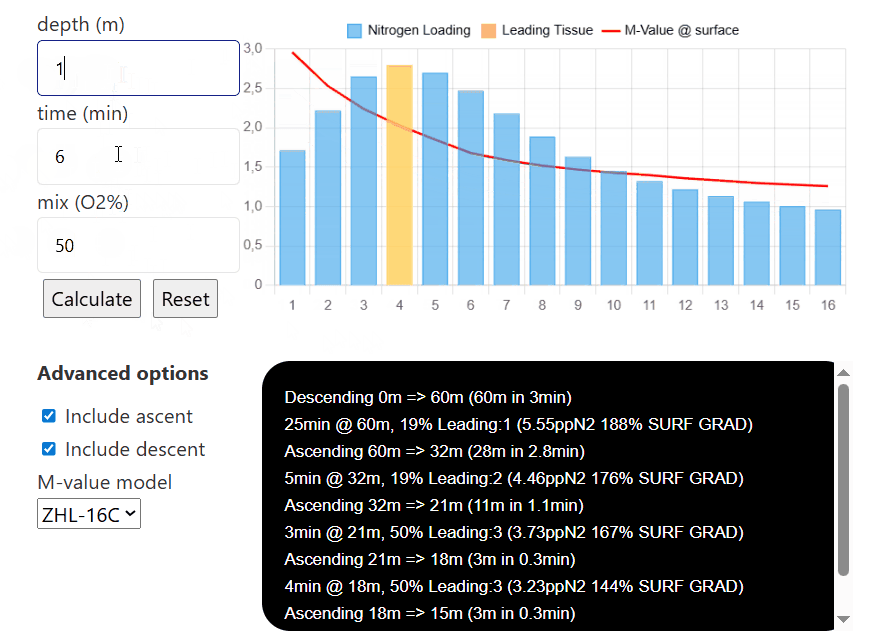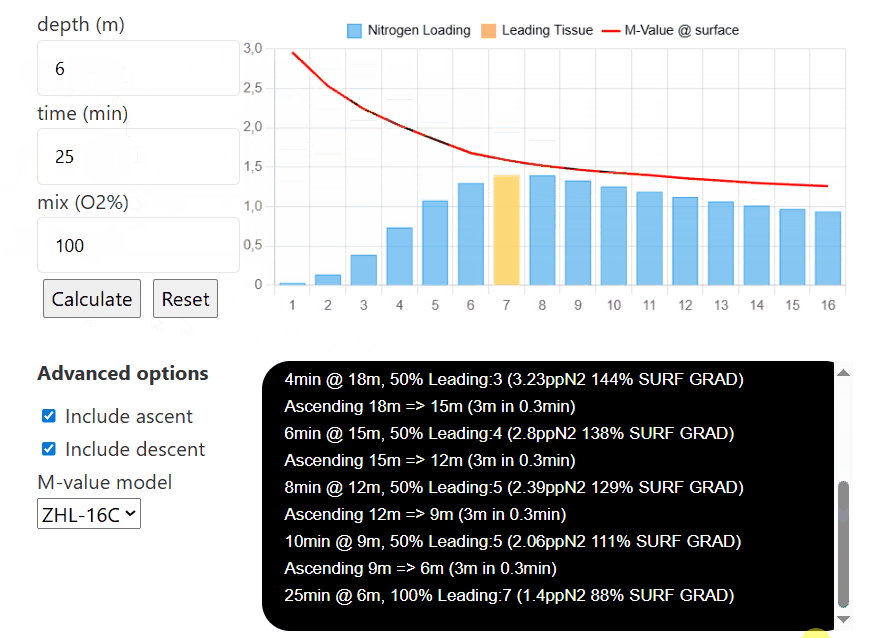
depth (m)
time (min)
mix (O2%)
Advanced options
What is the Nitrogen Loading Calculator?
The Nitrogen Loading calculator is a tool that allows you to visualize how your body saturates with nitrogen during your dive. By choosing a specific depth, bottom time, and gas mix (or a sequence of multiple depths, times, and mixes), this interactive tool allows visualization of the evolution of the nitrogen level in your tissues.
How to use this tool?
The interactive compartment saturation tool is designed with ease of use in mind. To start, input the depth you are aiming to go to, then input the time you are spending there, and finally, the mix you are choosing to breathe (the tool only considers nitrogen for now, and not any additional inert gases such as helium).
Then, once each tissue's nitrogen level is calculated, you can input different depths, times, and mixes (for example, to simulate consecutive decompression stops and visualize how they affect the nitrogen level in each individual compartment). Pressing reset will reinitialize all compartments to have
If you select the option to include ascent/descent, the model will calculate how the tissues saturate/desaturate while the diver moves between each depth (the default descent speed is 20m/min and the default ascent speed is 10m/min). If either option is unselected, the model will only calculate the sat/desat at that certain depth without taking the transition between depth into account.
What is a compartment?
Haldanian and Neo-Haldanian models consider that the tissues in our body are "compartmentalized". Intuitively, this means that instead of the nitrogen coming in and out of our body as one big block, it diffuses in different parts of our body at different speeds.
Those "different parts of our body" are hypothesized as theoretical compartments (or tissues) that each saturate/desaturate at a certain rate (some slower, some faster). Although the exact rate at which our real tissues on-gas/off-gas isn't known, theoretical half-times are assigned to each compartment: the first compartments (with a shorter half-time) will saturate faster, but will also desaturate faster; While the last compartments (with higher half-times), will saturate and desaturate slower.
You can imagine fast tissues being well-perfused tissues (meaning the tissues that have an abundant supply of blood flow or gas exchange), such as the lungs or the skin; while you can imagine the slow tissues being parts of your body that aren't as well-perfused and are a bit more "hidden", such as the bones, cartilage, tendons or even our fat!
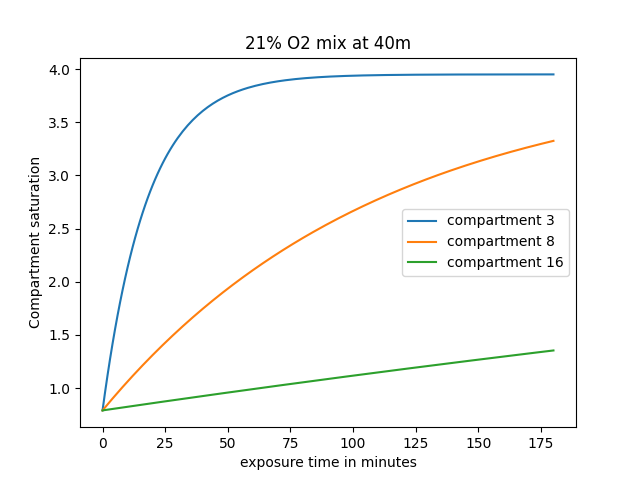
Below is an example of how fast different tissues saturate: in this example, we are looking at the compartments 3, 8, and 16; the diver goes to a depth of 40m while breathing air (21% Oxygen, 79% Nitrogen). The graph follows the evolution of each tissue's saturation level as the diver stays longer.
The following table shows the half-time of each tissue used in the calculations for the interactive tool:
compartment |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
half-time (min) |
5.0 | 8.0 | 12.5 | 18.5 | 27.0 | 38.3 | 54.3 | 77.0 | 109.0 | 146.0 | 187.0 | 239.0 | 305.0 | 390.0 | 498.0 | 635.0 |
How is the nitrogen level calculated?
Each compartment is calculated individually: using its start ppN2 pressure, the exposure time, the half-time of the tissue in question, and the partial pressure of the inhaled nitrogen, we can use the following equation (known as the Haldane equation) to calculate how much ppN2 each compartment is going to end up with:
\[P_{I,\text{ig}}(t_e) = P_{I,\text{ig}}(t_0) + (P_{gas,ig} - P_{I,\text{ig}}(t_0)) \cdot (1 - 2^{-t_e \over t_{I, 1/2}})\] \( P_{I,\text{ig}}(t_e): \text{Partial pressure of the inert gas dissolved in the compartment I} \\ \text{at the end of the exposure, expressed in bar} \) \(P_{I,\text{ig}}(t_0): \text{Partial pressure of the inert gas dissolved in the compartment I} \\ \text{before the exposure, expressed in bar} \) \(P_{gas,ig}: \text{Partial pressure of the inert gas in the breathing mix at ambient} \\ \text{pressure, expressed in bar} \) \(t_e: \text{duration of exposure, expressed in minutes}\) \(t_{I, 1/2}: \text{half time of the compartment I, expressed in minutes}\)For ascents and descents, a variant of that equation (called the Schreiner Equation) is used: we introduce a rate of change R, which denotes how much the partial pressure of the inert gas we are tracking (nitrogen in this case) changes per minute. For example, for an ascent of 10 meters per minute, breathing 21% oxygen, we would have:
R = 0.79 x -1 bar/min = -0.79 bar/min.\[P_{I,\text{ig}}(t_e) = P_{gas,ig} + R \cdot (t_e - {t_{I, 1/2} \over {\ln 2}}) - (P_{gas,ig} - P_{I,\text{ig}}(t_0) - {{R \cdot t_{I, 1/2}} \over {\ln 2}}) \cdot 2^{-t_e \over t_{I, 1/2}} \quad\] \(R: \text{rate of change of the partial pressure of the inert gas in the} \\ \text{breathing mix, expressed in bar/min}\)
